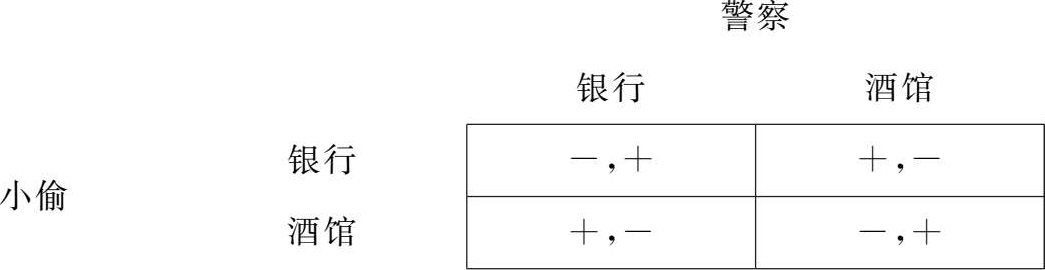
在西部片里，我们常能看到这样的故事：某个小镇上只有一名警察，他要负责整个镇的治安。现在我们假定，小镇的一头有一家酒馆，另一头有一家银行。再假定该地有一个小偷，要实施偷盗。因为分身乏术，警察一次只能在一个地方巡逻，而小偷也只能去一个地方。假定银行需要保护的财产价值为2万元，酒馆的财产价值为1万元。若警察在某地进行巡逻，而小偷也选择了去该地，就会被警察抓住；若警察没有巡逻的地方而小偷去了，则小偷偷盗成功。警察怎么巡逻才能使效果最好？

一个明显的做法是，警察对银行进行巡逻，这样，警察可以保住2万元的财产不被偷窃。可是如此，假如小偷去了酒馆，偷窃一定成功。这种做法是警察的最好做法吗？有没有对这种策略改进的措施？

这个博弈没有纯策略纳什均衡点，而实际上有混合策略均衡点。这个混合策略均衡点下的策略选择是每个博弈方的最优混合策略选择。那么，什么是混合策略呢？

策略是指博弈方在给定信息集的情况下选择行动的规则，它规定博弈方在什么情况下选择什么行动，是博弈方的“相机行动方案”。如果一个策略规定博弈方在每一个给定的信息情况下只选择一种特定的行动，该策略为纯策略。如果一个策略规定博弈方在给定信息情况下以某种概率分布随机地选择不同的行动，则该策略为混合策略。纯策略可视为混合策略的特例。在博弈中，博弈方可以改变他的策略，而使得他的策略选取满足一定的概率。当博弈是零和博弈时，即一方所得是另外一方的所失时，此时博弈只有混合策略均衡，对于任何一方来说，此时不可能有纯策略的占优策略。

在这个例子中，对于警察的一个最好的做法是，警察抽签决定去银行还是酒馆。因为银行的价值是酒馆的两倍，所以用两个签代表银行是合理的。比如，如果抽到1、2号签去银行，抽到3号签去酒馆。这样警察有2/3的机会去银行进行巡逻，1/3的机会去酒馆。而小偷的最优选择是：以同样抽签的办法决定去银行还是去酒馆偷盗，只是抽到1、2号签去酒馆，抽到3号签去银行，那么，小偷有l/3的机会去银行，2/3的机会去酒馆。这种方法正体现了混合策略的思想。

警察与小偷之间的博弈，如同我们孩提时代玩“石头-剪刀-布”的游戏，在这样一个游戏中，不存在纯策略均衡，对每个小孩来说，自己采取出“剪刀”、“布”或“石头”的策略应当是随机的，不能让对方知道自己的策略，哪怕是“倾向性”的策略，如果对方知道你出其中一个策略的“可能性”大，那么你在游戏中输的可能性就大。因此，在这样的博弈中，每个小孩的最优混合策略是采取每个策略的可能性是1/3，每个小孩都各取三个策略的1/3是纳什均衡。