智猪博弈说的是，有两头非常聪明的猪（要不怎么叫“智”猪呢），一大一小，共同生活在一个猪圈里。猪圈的一端有一个踏板，踏板连着开放饲料的机关，只要踏一下，在猪圈另外一端的食槽就会出现10个单位食物。经过精确的衡量，任何一头猪去踏这个踏板都会付出相当于2个单位食物的成本；每只猪都可以选择“踏”或“不踏”踏板。如果：

·两只猪一起去踏，然后一起回槽边进食，则大猪由于食得更快可吃下8个单位食物，小猪只能吃到2个单位食物，扣除各自的成本，大猪实际赢利6个单位食物，小猪则赢利0个单位食物；

·若大猪去踏，小猪先等候在食槽边，则大猪因时间耽搁只食得6个单位食物，小猪食得4个单位食物，大猪扣除成本后赢利4个单位食物，小猪没有成本因而赢利也为4个单位食物；

·若小猪去踏，大猪先候在槽边，则当小猪赶到槽边时大猪已经吃光了10个单位食物，小猪不仅什么都没吃到，反而还付出了2个单位成本；

·两只猪都不去踏，则大家都只能得到赢利0。

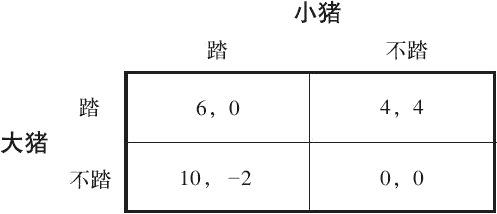
该博弈的赢利表如图4-1所示：

观察这个博弈可以发现：小猪有优势策略——无论大猪踏不踏，小猪选择不踏总是最合适的。（道理很简单：若大猪踏，则小猪踏得0，不踏得4；若大猪不踏，小猪踏得-2，不踏得0；即任何情况下均是不踏更好）。但是大猪没有优势策略，因为大猪的策略将随小猪策略的改变而改变，若小猪踏则大猪最好不踏（大猪踏得6，不踏得10），若小猪选择不踏则大猪最好选择踏（大猪踏得4，不踏得0）。

那么，这个博弈的稳定结果将是哪种情况呢？不妨这样考虑，既然不踏是小猪的优势策略，踏就是小猪的劣势策略。而劣势策略是参与人永远不会选择的，相当于小猪的策略集合里从来没有考虑过“踏”这一选项，因此可以把“踏”这个策略从小猪的策略集合中剔除。于是小猪只剩下唯一一个策略“不踏”。剔除劣势策略“踏”之后的赢利表就从图4-1变化为图4-2的形式：

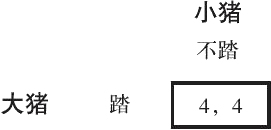
从图4-2中可以发现，在这个简化后的博弈中，对于大猪而言，踏是一个优势策略，而不踏是劣势策略。因此，我们可以继续剔除大猪的“不踏”策略，于是图4-2的简化博弈进一步简化成图4-3的形式：

经过第二轮剔除，我们得到了一个唯一的策略组合（踏，不踏），即大猪选择踏，小猪选择不踏。这个唯一的组合代表了它们策略行为唯一可收敛的情况，是一个稳定的结果。这种不断剔除劣势策略的方法，叫重复剔除劣势策略，所得到的稳定结果叫重复剔除劣势策略纳什均衡。

剔除劣势策略的一个重要前提思想是：理性的人永远不会选择其劣势策略。

智猪博弈深刻地反映了经济和社会生活中的免费搭车问题。无论大猪踏不踏，小猪都选择不踏（这是它的优势策略）；给定小猪不踏，大猪最好去踏。而且，有意思的是，大猪选择踏在主观上是为了自己的利益，但在客观上小猪也享受到了好处。这正是亚当·斯密“看不见的手”原理的一个童话版。看不见的手原理的意思是：社会上每个人为了自己的利益而采取行动，但这些行动在客观上也为社会上其他的人带来了好处。在经济学里，这头小猪被称为“搭便车者”。若全部的博弈主体都试图免费搭车，那么就可能陷入囚徒困境。在本章的前言中，弄堂两旁的居民好比是“小猪”，“小猪”没有动力去修路。后来，有了学校这头“大猪”介入，于是修路的重任就落到了学校这头“大猪”身上，当然那些作为“小猪”的居民也得到了好处。