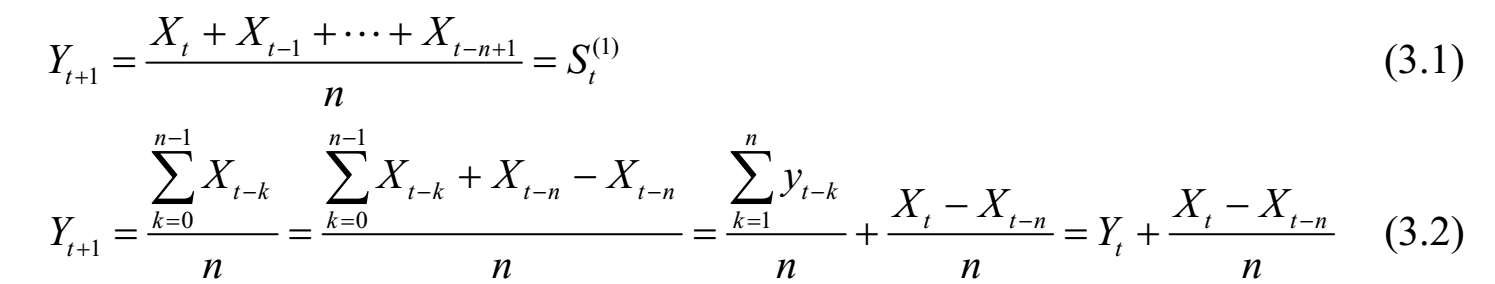一次移动平均预测是对原时间序列按一定的时间跨度逐项移动,形成一个新的时间序列,以消除短期的、偶然的因素引起的变动,显现出长期趋势。其过程可表述为:首先计算观察期的移动平均值;然后以上年的移动平均值为基准,计算各年移动平均值的趋势变动值;最后,将最后一年的移动平均值加上趋势增长值求出预测期的预测值。因此,移动平均法从数列中所取数据点数一直不变,只是包括最新的观察值。
(1) 一次移动平均法预测的原理。
设 X t为时间序列中时间点 t 的观测值,则在第 t 时点的移动平均值为 S t (1) ,其一次移动平均预测模型为
式中: X t——最新观察值; X t – n ——最早观察值; Y t +1 ——下一期的预测值; S t (1) ——第 t 期的一次移动平均值; n ——移动平均的项数。
式(3.2)说明,第 t +1期的预测值 Y t +1 是在第 t 期预测值 Y t的基础上加上一个修正项( X t- X t – n )/ n ,修正项的作用和 n 的大小有关。对于同样大小的变化量 X t- X t – n , n 越大,则|( X t- X t – n )/ n |越小,修正作用越小,对数据的平滑能力强。反之,若 n 越小,则修正作用越大,但平滑能力减小。因此,对 n 的选择不同,其预测的结果是不同的。一次移动平均预测法认为各期数据对将要发生的数据的影响是同等的。每次只能预测最近一期的数值,逐期移动,逐期预测。而且 n 值的选取有很大的随意性,预测精度较差,适合数据变化不大的近期预测。
在实际应用中,移动平均时段 n 的选择十分关键,它取决于预测目标和实际数据的变化规律。因此,不妨多取几个 n 值,对取不同的 n 值得出的预测结果分别同实际值相比较,计算其预测误差,最后选用预测误差最小的 n 值。从式(3.1)中可以看到,第 t 期的移动平均数只能作为 t +1期的预测值,如果要预测数期以后的值,这种方法就无能为力了。但是在实际预测中,当企业要逐月预测下个月的成百上千种产品的进货或销售情况时,这种方法还是很适用的。
一次移动平均法有两个优点:一是计算量少,二是能较好地反映时间序列的趋势及其变化。因此,尽管预测精度较低,目前在各种物流需求的预测中仍有较广泛的应用。
(2) 一次移动平均法应用举例。
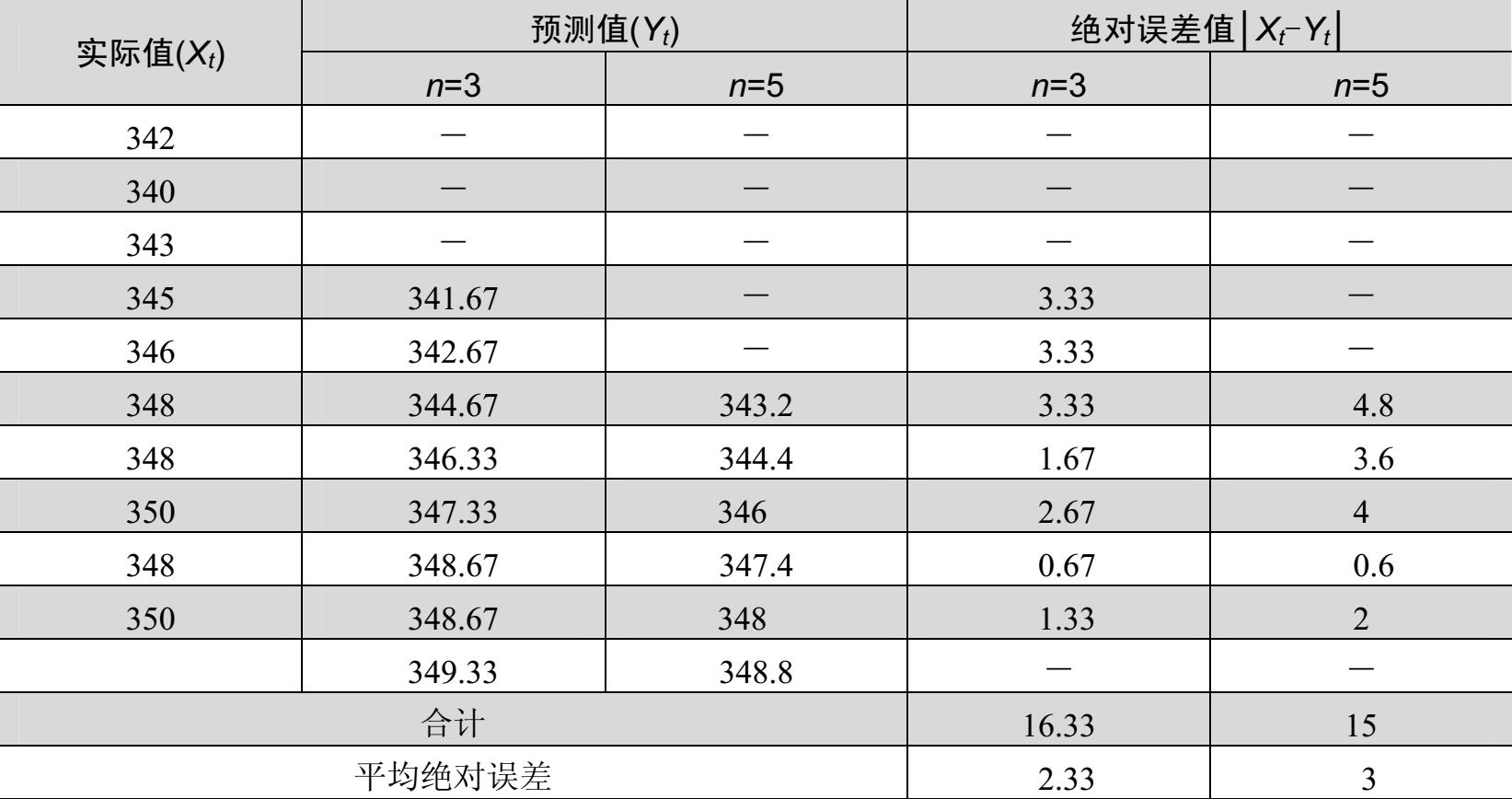
【例3.2】 某产品逐月需求量见表3-3,试用一次移动平均法预测该产品下个月的需求量。分别取n=3和n=5计算,并进行比较。
解:应用式(3.1)计算各时期的平均值,求出各预测值的绝对误差值和平均绝对误差值,见表3-3。
由表3-3的计算结果可知: n 值不同,各期的预测值也不同,预测误差也不同。当 n =3时,预测误差较小,因此,应选 n =3时的移动平均值作为预测值,即下一期的销售量预测值为349.33。
从例3.2的计算结果可以看出,简单移动平均预测对时间序列有修匀平滑的作用,但是它只能预测下一期的数值,对于远期数值的预测则无能为力,因此预测能力不强。另外,一次移动平均预测的结果存在滞后偏差,特别是在时间序列数据呈现线性趋势时,移动平均值总是落后于观察值数据的变化。因此,有必要引进二次移动平均预测,二次移动平均法可以纠正这一滞后偏差,建立预测目标的线性时间关系数学模型,求得预测值。
二次移动平均法是对一次移动平均数再进行第二次移动平均,再以一次移动平均值和二次移动平均值为基础建立预测模型,计算预测值的方法。二次移动平均预测不仅保留了一次平均移动预测的优点,还解决了一次移动平均预测只能预测下一期的局限性,它可以做近、短期的预测,适用于资料数据呈明显线性变化趋势的情况,其预测原理在这里不再赘述。但是,二次移动平均预测将近、远期的数据的重要性同等看待,这使预测精度受到了影响,为克服这个不足,引入加权移动平均法。